Question

Question 2 of 1010 PointsWhich inequality below satisfies the solution set graphed on the following number line?

Answer 1

C. x² - x ≥ 6

Step-by-step explanation

Let's analyze the solution set graphed first. We can see that the values -2 and 3 are included in the set, and all values below -2 and above 3. So, the solution set is (-∞, 2] U [3, ∞).

To find which inequality satisfies this solution set we have to solve them. To do so, we will be using the quadratic formula:

`\begin{gathered} ax^2+bx+c=0 \\ \\ x=(-b\pm√(b^2-4ac))/(2a) \end{gathered}`

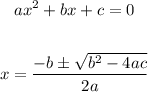
A. To solve this one, first, add x to both sides,

`-x^2+x+6\geqslant0`

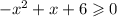
Now, apply the quadratic formula to find the zeros. For this inequality, a = -1, b = 1, and c = 6

`\begin{gathered} x=(-1\pm√(1^2-4(-1)6))/(2(-1))=(-1\pm√(1+24))/(-2)=(-1\pm√(25))/(-2) \\ \\ x_1=(-1-5)/(-2)=(-6)/(-2)=3 \\ \\ x_2=(-1+5)/(-2)=(4)/(-2)=-2 \end{gathered}`

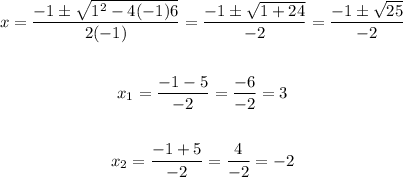
But in this case, the solution set is [-2, 3] - note that for any value outside this interval the inequality is false.

B. Similarly, apply the quadratic formula for a = -3, b = 3, c = 18,

`\begin{gathered} x=(-3\pm√(3^2-4(-3)18))/(2(-3))=(-3\pm√(9+216))/(2(-3))=(-3\pm√(225))/(-6)=(-3\pm15)/(-6) \\ \\ x_1=(-3+15)/(-6)=(12)/(-6)=-2 \\ \\ x_2=(-3-15)/(-6)=(-18)/(-6)=3 \end{gathered}`

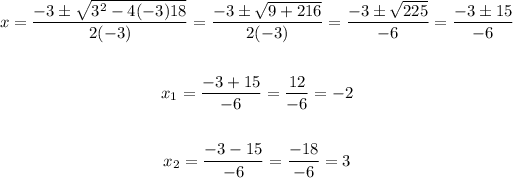
Again, the solution set is [-2, 3] since for any value outside the interval the inequality is not true.

C. Subtract 6 from both sides,

`x^2-x-6\geqslant0`

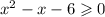
Apply the quadratic formula, with a = 1, b = -1, and c = -6,

`\begin{gathered} x=(-(-1)\pm√((-1)^2-4\cdot1(-6)))/(2\cdot1)=(1\pm√(1+24))/(2)=(1\pm√(25))/(2)=(1\pm5)/(2) \\ \\ x_1=(1+5)/(2)=(6)/(2)=3 \\ \\ x_2=(1-5)/(2)=(-4)/(2)=-2 \end{gathered}`

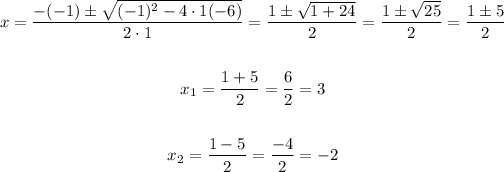
In this case, if we take any value between -2 and 3, for example 1,

`\begin{gathered} 1^2-1\ge6 \\ \\ 0\ge6 \end{gathered}`

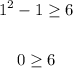
We can see that the inequality is false, while if we take a value greater than 3 or less than -2, for example, -5,

`\begin{gathered} (-5)^2-(-5)\ge6 \\ \\ 25+5\ge6 \\ \\ 30\ge6 \end{gathered}`

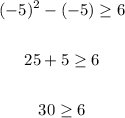
We can see that the inequality is true.

Hence, we can conclude that inequality C satisfies the solution set graphed.