Question

X - y ≥-3 and 3x + 2y ≥ 0

Answer 1

First, if we draw the lines of the equations x-y = -3 and 3x+2y = 0, we get the following:

the red line represents the first equation and the blue line represents the second equation. But since we are working with inequalities, the intersection between these two inequalities will be the intersection of the semiplanes that they form.

To check the region that will be the intersection, we can check two opposite points and see if both inequalities are true. In this case, if we take the points (-2,-2) and (2,2), we get the following:

`\begin{gathered} -2-(-2)\ge-3\text{ and }3(-2)+2(-2)\ge0 \\ \Rightarrow0\ge3\text{ and }-10\ge0 \end{gathered}`

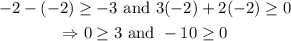
notice that the second inequality is not true. Now, with the point (2,2), we get:

`0=2-2\ge-3\text{ and }3(2)+2(2)\ge0`

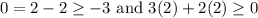
which are true, therefore, the region that represents both inequalities is the following: