Question

These box plots show the prices for two different brands of shoes.65 70 75 80 85Brand AHIH1550507085Brand B0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 e 90 95 100Price (5)Which statement is the most appropriate comparison of the spreads?O A. The interquartile range (IQR) for brand A, $10, is less than the IQRfor brand B, $20.O B. The interquartile ranges (IQRS) for brands A and B are both $20.O C. The median for brand A, $75, is greater than the median for brandB. $60.O D. The interquartile range (IQR) for brand A, $20, is less than the IQRfor brand B, $70.

Answer 1

Given:

Given the box plots of two different brands of shoes.

Required: Most appropriate comparison of the spreads

Step-by-step explanation:

From the box plot of brand A,

Minimum value = 65

First quartile, Q1 = 70

Median = 75

Third quartile, Q3 = 80

Maximum value = 85

Also, from the box plot of brand B,

Minimum value = 15

First quartile, Q1 = 50

Median = 60

Third quartile, Q3 = 70

Maximum value = 85

The interquartile range is the difference between the upper quartile and the lower quartile

The interquartile range of brand A is

`\begin{gathered} Q_3-Q_1=80-70 \\ =10 \end{gathered}`

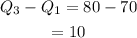
The interquartile range of brand B is

`\begin{gathered} Q_3-Q_1=70-50 \\ =20 \end{gathered}`

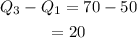
Option A is correct.

The median for brand A is $75, which is less than the median of brand B, $60.

Option C is correct.

Final Answer: The most appropriate