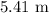Given:
the mass of the weight-watcher is
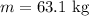
The work off equivalent to
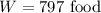
Required: height climbed by the person
Step-by-step explanation:
first we need to change the work into calories.
it is given that
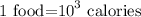
then the work done is
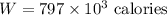
now change this work done from calories to joules.
we know that
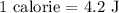
Then the work done is ,
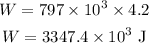
as the person climbs to the mountain the work done is stored as potential energy.
we assume that a person attained some height h,
then the work-energy relation,
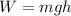
Plugging all the values in the above relation and solve for h, we get
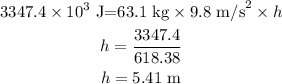
Thus, the height climbed by the person is