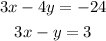Question

Choose the system of equations which matches the following graph:a line includes points 0 comma 6 and 4 comma 9. A line includes points 3 comma 6 and 2 comma 33x + 4y = 243x + y = −33x + 4y = 243x − y = 33x − 4y = −243x + y = −33x − 4y = −243x − y = 3

Answer 1

Step 1. The first line has the following two points:

(0, 6) and (4, 9)

The second line has the following points:

(3, 6) and (2, 3)

Step 2. To find the system of equations, we will need to find the line equation for each of the two lines.

To find the equations, we will first find the slope of the lines using the slope equation:

`\begin{gathered} slope: \\ m=(y_2-y_1)/(x_2-x_1) \end{gathered}`

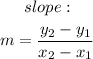
Where (x1, y1) and (x2, y2) are two points on the line.

Step 3. For the first line:

`\begin{gathered} (0,6)\rightarrow x_1=0,y_1=6 \\ (4,9)\rightarrow x_2=4,y_2=9 \end{gathered}`

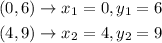
Therefore, the slope is:

`m=(9-6)/(4-0)=\boxed{(3)/(4)}`

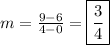
Step 4. For the second line:

`\begin{gathered} \left(3,6\right)\rightarrow x_1=3,y_1=6 \\ \left(2,3\right)\rightarrow x_2=2,y_2=3 \end{gathered}`

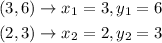
Therefore, the slope is:

`m=(3-6)/(2-3)=(-3)/(-1)=\boxed{3}`

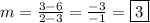
Step 5. Now, to find the equations, we will use the point-slope equation:

`y-y_1=m(x-x_1)`

Step 6. Substituting the values of (x1,y1) and m for the first line:

`y-6=(3)/(4)(x-0)`

Simplifying:

`\begin{gathered} y-6=(3)/(4)x \\ 4(y-6)=3x \\ 4y-24=3x \end{gathered}`

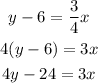
re-writing the equation to have the variables on the left-hand side:

`3x-4y=-24`

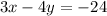
That is the equation of the first line.

Step 7. Substituting the values of (x1,y1) and m for the second line:

`\begin{gathered} y-y_(1)=m(x-x_(1)) \\ \downarrow \\ y-6=3(x-3) \end{gathered}`

Simplifying:

`y-6=3x-9`

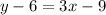
and rewriting the equation to have all of the terms on the left side:

`\begin{gathered} 3x-y=-6+9 \\ \downarrow \\ 3x-y=3 \end{gathered}`

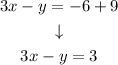
That is the equation of the second line.

Answer:

`\begin{gathered} 3x-4y=-24 \\ 3x-y=3 \end{gathered}`