Question

I need help please it says find the area of each shaded sector. Round to the nearest hundredth place.

Answer 1

Step 1

State the formula for the area of a sector of a circle

`A=(\theta)/(360)*\pi* r^2`

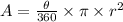
Step 2

Find the value of θ.

`m\angle WZV=\theta=180-108=72^{o^{}}(sum\text{ of angles on a straight line is }180^o)`

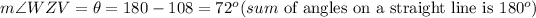
r=wz= 5.3km

Step 3

Find the area of the shaded part.

`\begin{gathered} A=(72)/(360)*\pi*(5.3)^2 \\ A=(1)/(5)*\pi*28.09 \\ A=(2809)/(500)(\pi)km^2 \end{gathered}`

Since there are 2 of such shaded sectors, they both will have the same area. Therefore the total area of the shaded sectors will be;

`\begin{gathered} (2809)/(500)(\pi)km^2*2 \\ =35.29893506 \\ \approx35.30km^2 \end{gathered}`

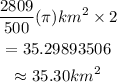
Answer; The area of the shaded sector approximately to the nearest hundredth is = 35.30km²