ANSWER :
The answers from column to column are :
g, h and s
e, a and b
d, q and r
k, f and c
m, l and n
EXPLANATION :
From the problem, we have the function :

The first column is the value of f(x) at given x values.
The second column is also the value of f(x) but written as a point (x, f(x))
The third column is the inverse of the function written as a point (f(x), x)
We will solve this from one column to another column.
That will be :
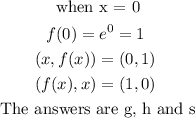
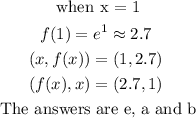
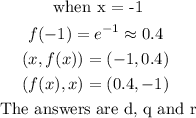


g, h and s