Given the table
If the slopes of the between the points are same, then it is a linear function.
Consider the two points (-2,0.2) and (0,2). Find the slope using the two point formula

The slope for the points (-2, 0.2 ) and (0, 2) is
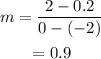
Consider the points (0, 2) and (2, 3.8). The slope for the points (0, 2) and (2, 3.8) is
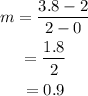
Consider the points (2, 3.8) and (4, 5.6). The slope for the points (2, 3.8) and (4, 5.6) is
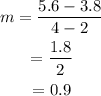
The slope is same for every consecutive pair of points. Hence the given function is linear.