Given the function below
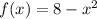
To determine the concavity of the graph of the given function
We calculate the average rate change of the given interval
The formula to find the average rate of change, A(x), change is
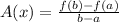
a) For the interval -1 ≤ x ≤ 1, the average rate of change, A(x) is
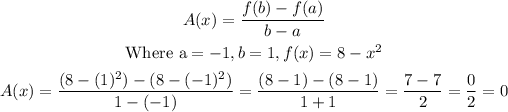
Hence, the average rate change over the interval -1 ≤ x ≤ 1 is 0
b) For the interval 1 ≤ x ≤ 3, the average rate of change, A(x) is
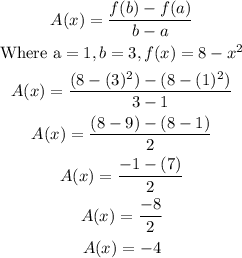
Hence, the average rate change over the interval 1 ≤ x ≤ 3 is -4
c) For the interval 3 ≤ x ≤ 5, the average rate of change, A(x) is
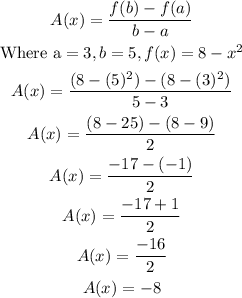
Hence, the average rate change over the interval 3 ≤ x ≤ 5 is -8
d) From the above deductions, the average rate of change is decreasing.
Hence, the graph of the function f(x) is Concave down