Question

What is the number of possible options for each situation?

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the method of getting possible options.

When asked to find the number of possible options, this is a permutation problem. Therefore, we use the permutation formula.

`^nP_r=(n!)/((n-r)!)`

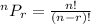
STEP 2: Solve the first question

`\begin{gathered} ^nP_r=(n!)/((n-r)!) \\ For\text{ the first question, n=}45,r=3 \\ ^(45)P_3=(45!)/((45-3)!)=(45!)/(42!)=(45*44*43*42!)/(42!) \\ \Rightarrow45*44*43=85140 \end{gathered}`

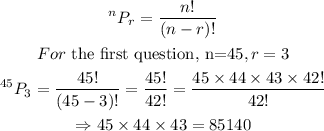
There are 85140 possible options.

STEP 3: Solve the second question

`\begin{gathered} ^nP_r=(n!)/((n-r)!) \\ n=7,r=5 \\ ^7P_5=(7!)/((7-5)!)=(7!)/(2!)=2520 \end{gathered}`

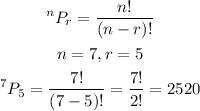
There are 2520 possible options.

STEP 4: Solve the third question.

`\begin{gathered} ^nP_r=(n!)/((n-r)!) \\ n=11,r=9 \\ ^(11)P_9=(11!)/((11-9)!)=(11!)/(2!)=19958400 \end{gathered}`

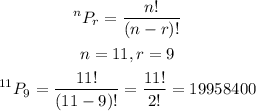
There are 19958400 possible options.

STEP 5: Solve the fourth question

`\begin{gathered} ^nP_r=(n!)/((n-r)!) \\ n=20,r=4 \\ ^(20)P_4=(20!)/((20-4)!)=(20!)/(16!)=(20*19*18*17*16!)/(16!)=20*19*18*17=116280 \end{gathered}`

There are 116280 possible options