Question

Find the perimeter as a radical expression in simplest form

Answer 1

The perimeter of the figure, in it's simplest form, is 2(1 + 5*sqrt(6)) feet

Explanation:

The perimeter of a figure is the sum of all dimensions of the figure.

In this question, the perimeter is:

`2+√(54)+√(54)+2√(24)`

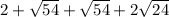
Adding like terms:

`2+√(54)+√(54)+2√(24)=2+2√(54)+2√(24)`

Now we have to factorize 54 and 24

Factorization of 54:

We go dividing by prime numbers.

54|2

27|3

9|3

3|3

1

So: 54 = 2*3*3*3 = 2*3³

Factorization of 24:

24|2

12|2

6|2

3|3

1

So 24 = 2*2*2*3=2³*3

Simplifying:

`2+2√(54)+2√(24)=2+2√(2\ast3^3)+2√(2^3\ast3)^{}`

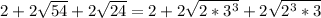
Now we continue working to place in the simplest form

`2+2√(2\ast3^3)+2√(2^3\ast3)=2+2√(2\ast3\ast3^2)+2√(2^2\ast2\ast3)`

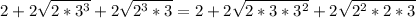
Now, for the radicals, we have that:

`√(2\ast3\ast3^2)=√(6\ast9)=√(6)\ast√(9)=3√(6)`
`√(2^2\ast2\ast3)=√(4\ast6)=√(4)\ast√(6)=2√(6)`

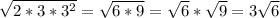
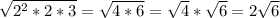
Then

`2+2√(2\ast3\ast3^2)+2√(2^2\ast2\ast3)=2+2\ast3√(6)+2\ast2√(6)`

Finally:

`2+2\ast3√(6)+2\ast2√(6)=2+6√(6)+4√(6)=2+10√(6)=2(1+5√(6))`

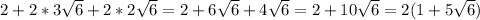
The perimeter of the figure, in it's simplest form, is 2(1 + 5*sqrt(6)) feet