Step 1
State the standard form of a hyperbola with the horizontal transverse axis with center at (0,0)
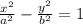
Step 2
For a hyperbola with the horizontal transverse axis with center at (0,0)

Points to work with include;

Step 3
Using points (50,-84) to find b²
We have;


Step 4
Solve for the x-coordinate of the right corner of the top
![\begin{gathered} The\text{ equation now becomes} \\ (x^2)/(24^2)-(36^2)/(2112.399168)=1 \\ (x^2)/(24^2)=1+(36^2)/(2112.399168) \\ (x^2)/(24^2)=(1265)/(784) \\ 784x^2=728640 \\ x^2=(728640)/(784) \\ x^2=(45540)/(49) \\ x=\sqrt[]{(45540)/(49)} \\ x=30.48586156 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2cme2u56i0o80qh5xosnuxlwyhcmc82eud.png)
But the diameter at the top = 2x
Therefore,
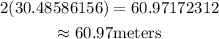
Hence approximately to 2, decimal places the diameter at the top = 60.97 meters