Question

Use Cramer's Rule to find the solution of the system of linear equations, if a unique solution exists.–5x + 2y – 2z = 263x + 5y + z = –22–3x – 5y – 2z = 21(–1, –7, 2)(–6, –1, 1)(–1, 3, 1)no unique solution

Answer 1

A system of three equations with three unknowns can be written in matrix form as shown below:

`\begin{gathered} a_1x+b_1y+c_1z=d_1 \\ a_2x+b_2y+c_2z=d_2 \\ a_3x+b_3y+c_3z=d_3 \\ \Leftrightarrow \\ \begin{bmatrix}{a_1} & {b_1} & {c_1} \\ {a_2} & {b_2} & {c_2} \\ {a_3} & {b_3} & {c_3}\end{bmatrix}\begin{bmatrix}{x} & {} & \\ {y} & {} & \\ {z} & {} & {}\end{bmatrix}=\begin{bmatrix}{d_1} & & {} \\ {d_2} & {} & {} \\ {d_3} & {} & {}\end{bmatrix} \end{gathered}`

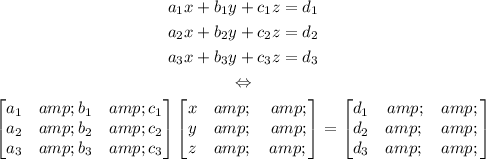
Then, x, y, and z are given by the expressions:

Then, in our problem:

`\begin{bmatrix}{-5_{}} & {2_{}} & {-2_{}} \\ {3_{}} & {5_{}} & {1_{}} \\ {-3_{}} & {-5_{}} & {-2_{}}\end{bmatrix}\begin{bmatrix}{x} & {} & \\ {y} & {} & \\ {z} & {} & {}\end{bmatrix}=\begin{bmatrix}{26_{}} & & {} \\ {-22_{}} & {} & {} \\ {21_{}} & {} & {}\end{bmatrix}`

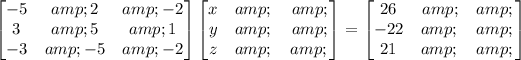
Therefore, x is equal to

`\begin{gathered} \Rightarrow x=\frac{\det(\begin{bmatrix}{26_{}} & {2_{}} & {-2_{}} \\ {-22_{}} & {5_{}} & {1_{}} \\ {21_{}} & {-5_{}} & {-2_{}}\end{bmatrix})}{\det(\begin{bmatrix}{-5_{}} & {2_{}} & {-2_{}} \\ {3_{}} & {5_{}} & {1_{}} \\ {-3_{}} & {-5_{}} & {-2_{}}\end{bmatrix})},=(-186)/(31)=-6 \\ \Rightarrow x=-6 \end{gathered}`

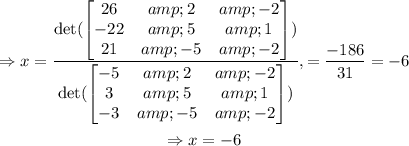
Therefore, x= -6

As for y,

`\begin{gathered} y=\frac{\det(\begin{bmatrix}{-5_{}} & {26_{}} & {-2_{}} \\ {3_{}} & {-22_{}} & {1_{}} \\ {-3_{}} & {21_{}} & {-2_{}}\end{bmatrix})}{\det(\begin{bmatrix}{-5_{}} & {2_{}} & {-2_{}} \\ {3_{}} & {5_{}} & {1_{}} \\ {-3_{}} & {-5_{}} & {-2_{}}\end{bmatrix})}=(-31)/(31)=-1 \\ \Rightarrow y=-1 \end{gathered}`

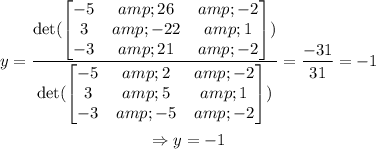
Thus, y= -1.

Finally solving for z:

`\begin{gathered} z=\frac{\det (\begin{bmatrix}{-5_{}} & {2_{}} & {26_{}} \\ {3_{}} & {5_{}} & {-22_{}} \\ {-3_{}} & {-5_{}} & {21_{}}\end{bmatrix})}{\det (\begin{bmatrix}{-5_{}} & {2_{}} & {-2_{}} \\ {3_{}} & {5_{}} & {1_{}} \\ {-3_{}} & {-5_{}} & {-2_{}}\end{bmatrix})}=(31)/(31)=1 \\ \Rightarrow z=1 \end{gathered}`

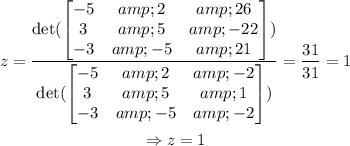
Hence, z=1

The answer is (-6, -1, 1)