Given data
*The given length of the rod is l = 2.00 m
*The given diameter of rod is d = 1.0 mm = 1.0 × 10^-3 m
*The elastic modulus of brass is E = 9.10 × 10^10 N/m^2
The formula for the spring constant of the rod is given as
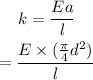
*Here a is the cross-sectional area of the rod
Substitute the known values in the above expression as
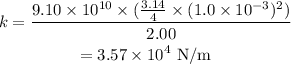
Hence, the spring constant of the rod is k = 3.57 × 10^4 N/m