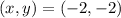We are given the following system of equations:
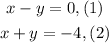
We are asked to determine the solution by graphing the system.
To do that we will graph each of the equations. We will solve for "y" in equation (1), to do that we will add "y" to both sides:

Switching the direction of the equation we get:

Now, we graph the equation. We notice that this is the equation of a line since it has the form:

In this case, m = 1 and b = 0.
To graph a line we need to know two points in the line. We will determine those points by giving values to "x". We will substitute the value x = 0, we get:

Substituting "x = 1" we get:
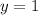
Therefore, the two points are:
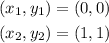
Now we plot both points and join them with a line. The graph is the following:
Now we solve for "y" in equation (2). To do that we will subtract "x" from both sides:

Now, we graph using the same procedure as before. We will graph both lines in the same coordinate system and we will determine their interception point, like this:
The interception point is the solution of the system. Therefore, the solution is: