Question

The revenue function R in terms of the number of units sold, a, is given as R= 380x - 0.1x^2where R is the total revenue in dollars. Find the number of units sold a that produces a maximum revenue?Your answer is x= What is the maximum revenue? __

Answer 1

Step-by-step explanation

The maximum revenue corresponds to the y-coordinate of the vertex of the graph of the revenue function. And the number of units sold that produces a maximum revenue corresponds to the x-coordinate of the vertex of the graph of the revenue function.

Then, we can find the vertex of the revenue function. For this, we can rewrite the function in its vertex form by completing the square.

`\begin{gathered} f(x)=ax^(^2)+bx+c\Rightarrow\text{ General form} \\ f(x)=a(x-h)^2+k\Rightarrow\text{ Vertex form} \\ \text{ Where }(h,k)\text{ is the vertex} \end{gathered}`

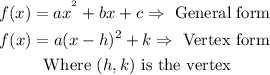
Then, we have:

Step 1: Reorder the terms.

`\begin{gathered} R=380x-0.1x^2 \\ R=-0.1x^2+380x \end{gathered}`

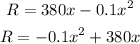
Step 2: We use the general form to find the values of a,b and c.

`\begin{gathered} a=-0.1 \\ b=380 \\ c=0 \end{gathered}`

Step 3: We find the value of h using the below formula.

`h=(-b)/(2a)`
`\begin{gathered} h=(-380)/(2(-0.1)) \\ h=(-380)/(-0.2) \\ h=1900 \end{gathered}`

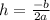
Step 4: We find the value of k using the below formula.

`k=c-(b^2)/(4a)`
`\begin{gathered} k=0-(380^2)/(4(-0.1)) \\ k=(-144400)/(-0.4) \\ k=361000 \end{gathered}`

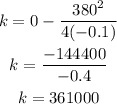
Step 5: We substitute the values of a, h and k into the vertex form.

`\begin{gathered} \begin{equation*} f(x)=a(x-h)^2+k \end{equation*} \\ R=-0.1(x-1900)^2+361000 \end{gathered}`

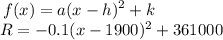
Thus, the vertex of the revenue function is the ordered pair (1900,361000).

Answer

The number of units sold that produces a maximum revenue is 1900, and the maximum revenue is $361000.