To find to polynomial from zeros.
Find the factors. If it is a positive zero, the factor will be (x- zero) If it is a negative zero if is (x+zero)
Multiply the factors together.
Zeros of 7, -7i would be:
Find the factors:

Multiply the factors together: Will start out with FOIL for (x-7)(x+-7i) =
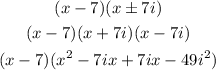
Combine like terms. Then multiply by the last factor

Therefore the correct answer from the Option is D