Question

Select the correct choice below and fill in any answer boxes in your choice.

Answer 1

To answer this equation we must first simplify it and apply the general rule of math when it comes to dealing with equations.

Remember the rule that, whatever you do on the left side of the equation you must do the same to the other side.

Let's start.

We are given the equation:

`8x-(5x+2)=5x-12`

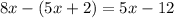
Now for our first step let us simplify the left side of the equation first. Since we have a parenthesis in our equation let us remove it by distributing the negative (-) sign outside the parenthesis into the terms inside the parenthesis.

`8x-5x-2=5x-12`

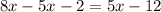
Notice that we can combine 8x and -5x since they are like terms.

`\begin{gathered} 8x-5x-2=5x-12 \\ 3x-2=5x-12 \end{gathered}`

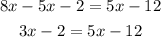
Now we have simplified the left side of the equation and looking at the right side, it can't be simplified further.

Now let us evaluate the equation to find the value of x. Looking at our new equation which is:

`3x-2=5x-12`

We can see that both terms with the same variable are separated, so let us manoeuvre so that they can be together on the same side of the equation.

To do that let us subtract 3x in the left side of our equation in order to cancel the original 3x in there, and do the same to the right side of the equation by the virtue of the general rule we talked about earlier. Now we have an equation that looks like this:

`3x-2-3x=5x-12-3x`

Notice that 3x and -3x on the left side of our equation can be cancelled since they will just add up to 0. And the 5x and -3x on the right side of the equation can be combined since they have like terms. Now our equation becomes:

`-2=2x-12`

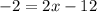
Now let us do the same thing to the -12 in the right side of the equation, let us transfer it to the left side of the equation so that we can combine it with -2.

To do that we only have to add 12 on the right side of the equation to cancel out the -12, and do the same to the left side of the equation. Our equation now becomes:

`-2+12=2x-12+12`

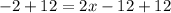
Notice again that 12 and -12 on the right side can be cancelled out since they are just equal to 0. And -2 and 12 can be combined since they are like terms. Now our equation becomes:

`10=2x`

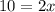
Now we have simplified our equation to its simplest form it is now time to evaluate the equation. To do that simply divide both sides by 2 so that only x remains on the right side of the equation, and we can now know the value of x.

`\begin{gathered} (10)/(2)=(2x)/(2) \\ 5=x \\ x=5 \end{gathered}`

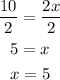
Therefore the value of our x is 5.

Therefore the answer to our question is LETTER A. The solution set is {5}.