Answer
The limit of the series is ∞
Step-by-step explanation
Problem Statement
We are asked to find the limit of the following infinite series

Solution
Step 1: Check for a finite number of terms
- In order for us to find the limit of the series, it is important for us to know if the sequence of the terms of the series is convergent. If the sequence of the terms is convergent, then, perhaps the series could be convergent as well.
- Finding the convergence of the terms of the series, we have:

- This means that the terms of the series converge to zero eventually.
- This gives us a reason to think the series can have a limit since the terms of the series are not infinite.
Step 2: Check the convergence of the sum of the series itself
- This time, we would like to know if the sum of the series is convergent.
- if the sum of the series can be known to be convergent ahead of time, then, we can know for certain that the sum to infinity of the series exists and is a finite value.
- The way we shall approach this is by applying the Series Integral test. This test has some constraints which are:
1. The series must be continuous on the interval [1, ∞]
2. The series must be positive on the interval [1, ∞]
3. The series must be decreasing on the interval [1, ∞].
For constraint 1, for all values of n, the series has real number terms, therefore, it is continuous.
For constraint 2, since n is greater than or equal to 1, the numerator and denominator will always be positive, implying that the overall fraction is positive for all values over the interval [1, ∞].
For constraint 3, we already showed how the terms of the series converge to zero in Step 1 above. This implies that the series is a decreasing series over the interval [1, ∞].
- Now that we have satisfied all the constraints of the Series Integral test, we can now apply the test itself.
- The Series Integral test states that:
"If the 3 constraints listed above are met, then
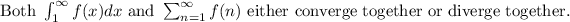
- This means we can simply integrate the function representation of the series expression and apply the boundary conditions. If the answer is a finite value, then, the series itself converges but if the answer is infinite, then the series itself diverges.
- Applying this Series Integral test, we have:
![\begin{gathered} f(n)=(3n^5)/(6n^6+1) \\ \therefore f(x)=(3x^5)/(6x^6+1) \\ \\ \int ^(\infty)_1f(x)dx=\int ^(\infty)_1(3x^5)/(6x^6+1)dx \\ \\ \text{ We can solve this using U-substitution} \\ \text{Let }u=6x^6+1 \\ \text{Differentiate u with respect to x} \\ \mathrm{(du)/(dx)}=\mathrm{(d)/(dx)}({\mathrm{6x}^{\mathrm{6}}}\mathrm{+1}) \\ \mathrm{(du)/(dx)}=6*6x^5=36x^5 \\ \\ \therefore\mathrm{dx}=(du)/(36x^5) \\ \\ \text{ Substitute the expression for u and }dx\text{ into the integral} \\ \int ^(\infty)_1(3x^5)/(6x^6+1)dx=\int ^(\infty)_1(3x^5)/(u)(du)/(36x^5) \\ \\ \text{This simplifies to:} \\ \int ^(\infty)_1(1)/(u)(du)/(12)=(1)/(12)\int ^(\infty)_1(1)/(u)du \\ \\ \text{ The integral becomes:} \\ (1)/(12)(\ln u)|^(\infty)_1 \\ \\ \text{ Substitute the expression for u into the result above} \\ (1)/(12)(\ln (6x^6+1))|^(\infty)_1 \\ \\ \text{Applying the boundary conditions} \\ (1)/(12)(\ln (6\infty^6+1)-\ln (6(1)^6+1) \\ \\ =(1)/(12)(\infty-\ln 7) \\ \\ \therefore\int ^(\infty)_1(3x^5)/(6x^6+1)dx=\infty \end{gathered}]()
- We can see that the Series Integral Test returns an infinite value.
- This means that the series diverges.
Final Answer
The limit of the series is ∞