Question

Find the area of the sector, given central angle of 70 degrees and a radius of 6. Leave your answer in terms of π.

Answer 1

The rule of the area of a sector which has radius r and central angle x degrees is

`A=(x)/(360)*\pi r^2`

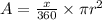
Since the central angle is 70 degrees, then

`x=70^(\circ)`

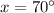
Since the radius of the circle is 6, then

`r=6`

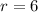
Substitute them in the rule above

`\begin{gathered} A=(70)/(360)*\pi*6^2 \\ \\ A=(70)/(360)*\pi*36 \\ \\ A=7\pi \end{gathered}`

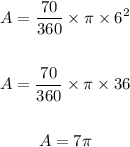
The answer is

The area of the sector is 7pi square units