Given
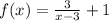
The vertical asymptotes are given by the value of x which makes the denominator equal to zero. In our case,
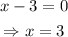
Thus, the vertical asymptote is x=3.
As for the horizontal asymptote, notice that
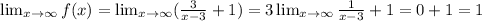
Similarly,
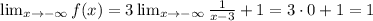
Therefore, the horizontal asymptote is y=1.
As for the domain of the function, the only points that are not included in the domain are those that cause a vertical asymptote. Hence,

Similarly, since y=1 is a horizontal asymptote,
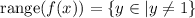
Thus, the domain is all real numbers except 3, and the range is all real numbers except 1.