Equilateral Triangle : An equilateral triangle is a triangle that has all its sides equal in length. Also, the three angles of the equilateral triangle are congruent and equal to 60 degrees.
Triangle ABC is an equilateral triangle so,
All the sides are equal and the angles are of 60 degree
Angle A = Angle B= Angle D = 60
The line AC divides the triangle ABD into two equal parts So, the angle A also divided in two equal parts
Since:
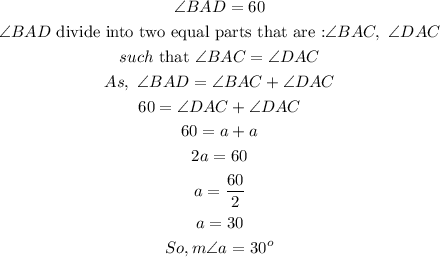
m
Since m beacuse ABD is an equilateral triangle
AC divide the triangle in two equal parts
So, the line segment BD is divided into two equal parts by the point C
So, BC = CD
From the given figure we have BC =4, CD=e
So, BC = CD = 4
CD = e = 4
e= 4
The length of the side BD = BC + CD
BD = 4 + e
BD = 4 + 4
BD = 8
Since the triangle ABD is an equilateral triangle all sides are equal :
So, AB = BD = DA
AB = 8 = DA
AB = 8 = c
c = 8
The line AC makes 90 degree to the line BD
Thus, the triangle ACD is a right angle triangle
Apply pythagoras theorem:
Pythagoras Theorem: In a right angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides.
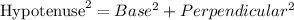
In the given triangle ACD we have :
Hypotenuse AD = 8, base CD = 4,
Perpendicular AC =f
Substitute the value and solve for AC=f
![\begin{gathered} \text{Hypotenuse}^2=Base^2+Perpendicular^2 \\ AD^2=CD^2+f^2 \\ 8^2=4^2+f^2 \\ 64=16+f^2 \\ f^2=64-16 \\ f^2=48 \\ f=\sqrt[]{48} \\ f=\sqrt[]{2*2*2*2*3} \\ f=\sqrt[]{2^2*2^2*3} \\ f=2*2\sqrt[]{3} \\ f=4\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rk2za4bbknmb3r1b8g0vaovllfsieozlu4.png)
f = 4 square root of 3
Answer :
m
m
c = 8
e= 4
f = 4 square root of 3