Question

One month lashonda rented 3 movies and 2 video games for a total of $19. The next month she rented 5 movies and 6 video games for a total of $47. Find the rental cost for each movie and each video game

Answer 1

We are given that:

Lashonda rented 3 movies and 2 video games for a total of $19. If "x" is the cost per movie and "y" the cost per video game, then we can write this mathematically as:

`3x+2y=19,(1)`

This is our first equation.

We are also given that:

She rented 5 movies and 6 video games for a total of $47. This can be written mathematically as:

`5x+6y=47,(2)`

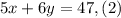
This is our second equation.

To solve the system we will solve for "x" in equation (1). To do that we will subtract "2y" from both sides:

`3x=19-2y`

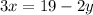
Now we divide both sides by 3:

`x=(19-2y)/(3)`

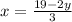
Now we substitute this in equation (1):

`5((19-2y)/(3))+6y=47`

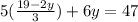
Now we use the distributive law on the parenthesis:

`(95-10y)/(3)+6y=47`

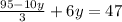
Now we multiply both sides by 3, we get:

`95-10y+18y=141`

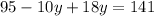
Now we add like terms:

`95+8y=141`

Now, we subtract 95 from both sides:

`\begin{gathered} 8y=141-95 \\ 8y=46 \end{gathered}`

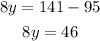
Dividing both sides by 8:

`y=(46)/(8)=5.75`

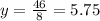
Now we substitute this value in equation (1), the one where we have solved for "x", we get:

`x=(19-2(5.75))/(3)`

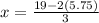
Solving the operations we get:

`x=2.5`

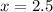
Therefore, each movie costs $2.5 and each video game costs $5.75.