Question

Given Pr (E) = 0.25, Pr (F) = 0.84, and Pr (E U F) = 0.85.a.What's Pr (E n F)?b.Are event E and event F mutually exclusive? Justify your answer.C.Are event E and event F independent? Justify your answer.

Answer 1

Step-by-step explanation:

a) Here, we want to get the probability of the intersection of the two events

Mathematically, we know that:

`P(E\text{ U F) = P(E) + P(F) - P(E n F)}`

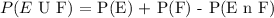
Substituting the values we have:

`\begin{gathered} 0.85\text{ = 0.25 + 0.84 }-\text{ P(E n F)} \\ P(E\text{ n F) = 0.25 + 0.84 - 0.85} \\ P(E\text{ n F) = 0.24} \end{gathered}`

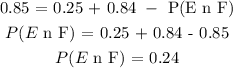
b) We want to check if the two events aree mutually exclusive

For two events to be mutually exclusive, the intersection of both does not exist. What this mean factually is that the intersection of both is zero. But from our calculations, this is false. Hence, the events are not mutually exclusive as they are not disjoint

c) We want to check if the events are independent

For independent events, we have it that:

`P(\text{ A n B) = P(A) }*\text{ P(B)}`

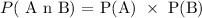
With respect to the question we have:

`\begin{gathered} P(E\text{ n F) = P(E) }*\text{ P(F)} \\ 0.24\text{ }\\e\text{ 0.25 }*\text{ 0.84} \end{gathered}`

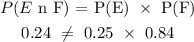
Since the intersection of both is not equal to their product, then the events are not independent

In practice, these events are termed to be mutually inclusive (They are neither independent nor mutually exclusive)