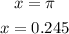Given the equation;
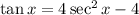
We start by moving all terms to the left side of the equation;
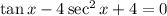
Now we re-write this using trig identities;

Note that;
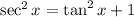
Input this into the last equation and we'll have;
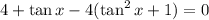
Simplify the parenthesis;
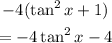
We now refine the last equation;
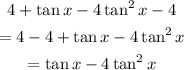
The equation now becomes;
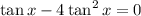
We now represent tan x by letter a.
That means;
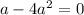
We shall apply the rule;
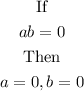
Therefore;
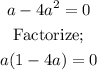
At this point the solutions are;
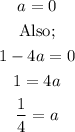
If we now substitute a = tan x back into the equation, we would have;

Where tan x = 0;
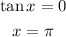
Where tan x = 1/4;
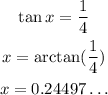
ANSWER: