In one year, there are 365 days. In one day, there are 24 hours.
The number of minutes in an year is,
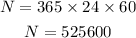
The Perseid meteor appear every 1 1/5 minutes.
The number of Perseid meteors in one year is,
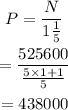
The Leonid meteor appear every 4 2/3 minutes.
The number of Leonid meteors showered in one year is,
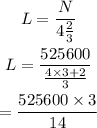
The number of Persoid meteors more than the Leonid meteors is,
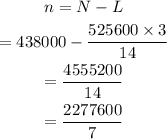
Let m be the number of times Persoid meteors is more than the Leonid meteors in each minute. Then,
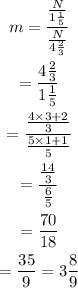
Therefore, Persoid meteors is 3 8/9 times more than the Leonid meteors showered in each minute