Based on the information given in the exercise, you can set up the following System of equations:
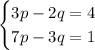
You can use the Substitution method to find the value of the variable "p" and the variable "q":
- Solve for "q" from the first equation:
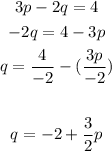
- Substitute the new equation into the second equation:
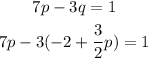
- Solve for "p":
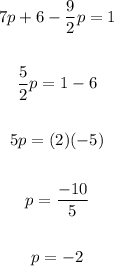
- Substitute the value of "p" into the equation
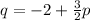
And evaluate. Then:
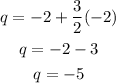
Now knowing the values of "p" and "q", you can substitute them into this expression:

And then evaluate. So, you get:
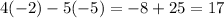
Therefore:
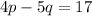
The answer is: Option D.