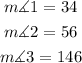
Step-by-step explanation
Step 1
as the horizontal lines are parallel, the angles (1) and x are congruents, so
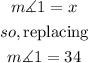
Step 2
Now, we can see that angles (1) and (2) are complementary angesl (When two angles add to 90°)
so

Step 3
finally, angles (1) and angle (3) are supplementary angles (Two Angles are Supplementary when they add up to 180 degrees)
so
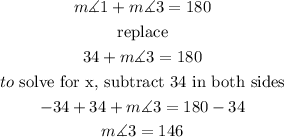
i hope this helps you