Answer:
45 times
Step-by-step explanation:
A six-sided number cube has the following numbers written on its six faces.
1, 2, 3, 4, 5, 6
As can be seen, three of the above numbers (1, 3 and 5) are odd. This means that half of the cube faces have odd numbers printed on them.
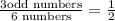
Therefore, the probability that a toss would land on an odd number is 1/2 or 50%.
Now if we do 90 tosses, then we expect that 50% of them would give us an odd number.
Therefore, the number of tosses we expect to give an odd number is

Hence, we expect the number cube to give us odd numbers 45 times out of 90 tosses.