Given:
The mass of the truck is m1 = 912 kg
The initial velocity of the truck is

The mass of the car is m2 = 618 kg
The initial velocity of the car is
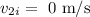
To find the velocity of the truck and car after the collision.
Step-by-step explanation:
According to the conservation of momentum,
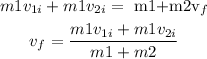
On substituting the values, the magnitude of velocity after the collision will be
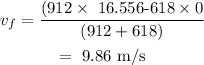
Thus, the magnitude of velocity after the collison is 9.86 m/s