Question

Choose the system of equations that matches the following graph:a line with (0, 6) and (4, 9).A line with (3, 6) and (2, 3).3x + 4y = 243x + y = −33x + 4y = 243x − y = 33x − 4y = −243x + y = −33x − 4y = −243x − y = 3

Answer 1

In order to find the correct system, let's find the equation of each line.

To do so, first let's find the slope of each line with the formula below:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1)\\ \\ \\ \\ m_1=(9-6)/(4-0)=(3)/(4)\\ \\ \\ \\ m_2=(3-6)/(2-3)=(-3)/(-1)=3 \end{gathered}`

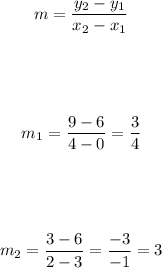
Now, let's use the point-slope formula and then rewrite in the standard form:

`\begin{gathered} (y-y_1)=m(x-x_1)\\ \\ \\ \\ point\text{ \lparen0,6\rparen }and\text{ m=3/4}\\ \\ (y-6)=(3)/(4)(x-0)\\ \\ y-6=(3)/(4)x\\ \\ 4y-24=3x\\ \\ 3x-4y=-24\\ \\ \\ \\ point\text{ \lparen3,6\rparen }and\text{ m=3}\\ \\ (y-6)=3(x-3)\\ \\ y-6=3x-9\\ \\ 3x-y=3 \end{gathered}`

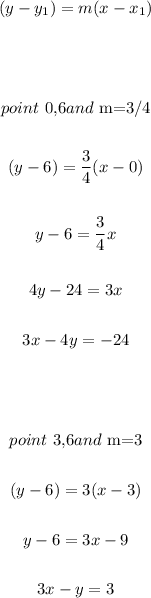
The equations are 3x - 4y = -24 and 3x - y = 3, therefore the correct system is the fourth one.