Answer: We have to find the JK, the simple answer is as follows, it is calculated by first finding the angle M and then using a trigonometric ratio to calculate the JK.
The simple and brief steps are as follows:
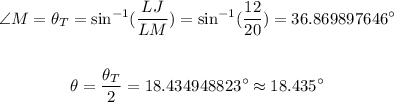
Therefore the JK is:
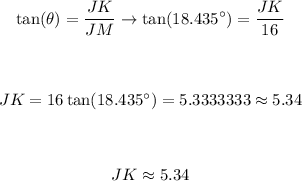
Therefore JK is 5.34.