Recall that the x-intercepts of a graph are of the form:
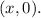
Since the graph of f(x) passes through (0,0), (1, -2), and (2,0), then its x-intercepts are (0,0) and (2,0).
Therefore f(x) must be as follows:
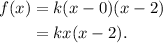
Where k is a constant.
Since f(x) passes through (1,-2), then:
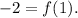
Then:

Simplifying the above equation we get:
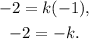
Therefore:
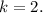
Therefore f(x) could be as follows:
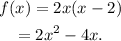
Answer: First option.