Question

Recently, More Money 4U offered an annuity that pays 4.5% compounded monthly. If $1,643 is deposited into this annuity every month, how much is in the accountols after 11 years? How much of this is interest?

Answer 1

The rule of the FV (future value) is

`FV=P((1+i)^n-1)/(i)`

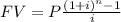
P is the value each month

i is the rate divided by 12 month

n = number of years x 12 months

Since the deposit every month is $1643, then

`P=1643`

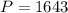
Since the annuity rate is 4.5%, then

`\begin{gathered} i=(4.5)/(12)=0.375\text{ \%} \\ i=(0.375)/(100)=0.00375 \end{gathered}`

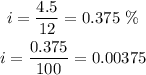
Since the number of years is 11 years, then

`\begin{gathered} n=11*12 \\ n=132 \end{gathered}`

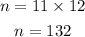
Substitute them in the rule above

`\begin{gathered} FV=1643((1+0.00375)^(132)-1)/(0.00375) \\ FV=279958.5032 \end{gathered}`

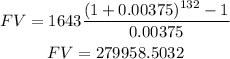
The account will have $279,959 after 11 years to the nearest dollar

To find the interest subtract $1643 x 132 months from the FV

`\begin{gathered} I=FV-n* P \\ I=279959-132*1643 \\ I=63083 \end{gathered}`

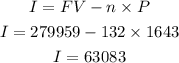
The amount of interest is $63,083 to the nearest dollar