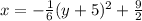Answer:
Step-by-step explanation:
Given a parabola such that:
• The directrix, x=6
,
• Focus = (3, -5)
The standard form of a left-right parabola is given as:

The focus is obtained using the formula:
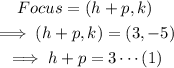
The directrix is obtained using the formula:

Solve equations 1 and 2 simultaneously:
![\begin{gathered} \begin{equation*} h+p=3\cdots(1) \end{equation*} \\ h-p=6\operatorname{\cdots}(2) \\ Add \\ 2h=9 \\ h=4.5 \\ \text{ Solve for p} \\ 4.5+p=3 \\ p=3-4.5 \\ p=-1.5 \end{gathered}]()
Substitute into the standard form:
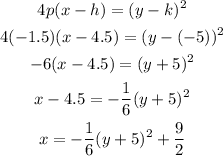
The vertex form of the parabola is: