Question

Is the triangle with the vertices A(7,3), B(0,7), and C(-8, -7) a right triangle?Is the triangle a right triangle?O YesO No

Answer 1

We want to use coordinate geometry to determine if the triangle is a right triangle

We can find the distance between all the three vertices.

The formula for distance between two points ( x1 , y1 ) and ( x2, y2) is given as :

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

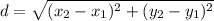
Let us start by finding the distance AB

Let us find the distance BC

Now let us find the distance AC

The triangle will be a right triangle if it obeys pythagoras theorem

Pythagoras' theorem says if we square the longest side in a right triangle , then it must be equal to the sum of the squares of the other two sides

Let us see if that works. If it works, the triangle is right triangle. If it doesn't work, we conclude otherwise.

So we can say that only right triangle obeys pythagoras' theorem.

Now lets verify

Longest side is AC

`AC=5√(13)`

`\begin{gathered} AC^2=(5√(13)^2)=\text{ }5√(13)*5√(13)=325 \\ AC^2=325 \end{gathered}`

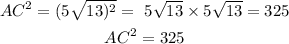
Let us find the sum of the squares of AB and BC

`\begin{gathered} AB^2+BC^2=√(65^2)+(2√(65))^2 \\ AB^2+BC^2=65+260=325 \end{gathered}`

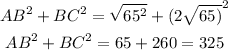
Now we observe that ;

`AC^2=AB^2+BC^2`

The triangle given is a right triangle

Our choice is Yes