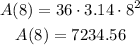In this problem the expression that represente the paint in terms of time is:
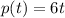
and the area is represent as:
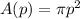
Part A: So to have the area in terms of p we can replace the first equation in the secon one so wi will get:
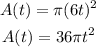
Part B: now we can replace the 8 minutes in the equation so we get: