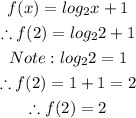The given function is,
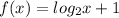
The graph of the function will be plotted below
A vertical asymptote is a vertical line that guides the graph of the function but is not part of it.
Hence, the vertical asymptote is at
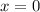
The domain of a function f(x) is the set of all values for which the function is defined.
Hence, the domain of the function is
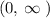
The range of a function is the complete set of all possible resulting values of the dependent variable.
Hence, the range of the function is
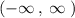
Let get the f(x), when x = 2