Question

Determine whether the given information results in one triangle or two. a=6, b=2, A=20 degrees

Answer 1

Given:

a = 6

b = 2

A = 20 degrees

a.) Let's determine Angle B. Apply the Sine Law.

`\text{ }\frac{a}{S\text{ine A}}\text{ = }\frac{b}{S\text{ine B}}`
`\text{ }\frac{6}{S\text{ine }20^(\circ)}\text{ = }\frac{2}{S\text{ine B}}`
`\text{ Sine B = }((2)(Sine20^(\circ)))/(6)\text{ = 0.11400671444}`
`\text{ B = Sine}^(-1)(\text{0.11400671444)}`
`\text{ B }\approx6.55^(\circ)`

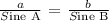
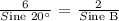
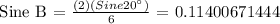
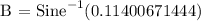
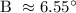
b.) Let's find Angle C.

`\angle A\text{ + }\angle B\text{ + }\angle C=180^(\circ)`
`20^(\circ)+6.55^(\circ)\text{ + }\angle C=180^(\circ)`
`\angle C+26.55^(\circ)=180^(\circ)`
`\angle C=180^(\circ)\text{ - }26.55^(\circ)`
`\text{ }\angle C=153.45^(\circ)`

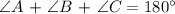
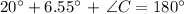
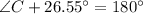
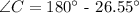
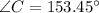
Therefore, the measure of Angle C is 153.45 degrees.

c.) Let's determine the length of side c. Apply the Sine Law.

`\text{ }\frac{6}{S\text{ine }20^(\circ)}\text{ = }\frac{c}{S\text{ine }153.45^(\circ)}`
`c\text{ = }\frac{(6)(S\text{ine }153.45^(\circ))}{S\text{ine }20^(\circ)}`
`c\text{ }\approx\text{ 7.84}`

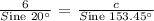
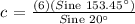
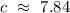
In Summary, the information results in one triangle with the following details:

a = 6

b = 2

c = 7.84

A = 20 degrees

B = 6.55 degrees

C = 153.45 degress