The parabola equation in vertex form is given by:

From the given question, we are provided with the following:
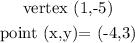
We have to use the given parameters to find the parameter 'a' from the parabola equation.
Thus, we have:

Hence, the equation of the parabola is:

The graph of the parabola on the xy-plane is shown below: