Question

Express (4x3 + 5x + 1)/(x2 + 1) using long division method in the form q(x) + r(x)/b(x) where q(x) is the quotient, r(x) is the remainder, and b(x) is the divisor.

Answer 1

4x + (x + 1) / (x^2 + 1)

Step-by-step explanation:

We perform the long division

The result of the above long division tells is that

`4x^3+5x+1=4x(x^2+1)+(x+1)`

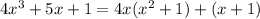
If we now divide both sides by x^2 + 1, we get

`(4x^3+5x+1)/(x^2+1)=(4x(x^2+1)+(x+1))/(x^2+1)`
`=(4x(x^2+1))/(x^2+1)+((x+1))/(x^2+1)`
`=4x+(x+1)/(x^2+1)`

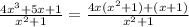
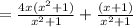
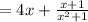
Hence,

`\boxed{(4x^3+5x+1)/(x^2+1)=4x+(x+1)/(x^2+1)\text{.}}`

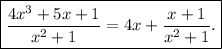
Therefore, the first choice from the options is the correct answer!