We are asked to determine the area of a circular sector. To do that we will use the following formula:
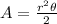
Where:
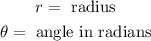
Now, we convert the angle of 85° to radians using the following conversion factor:
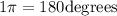
Now, we multiply by the conversion factor:
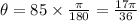
Now, we substitute in the formula for the area:
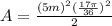
Substituting the value of pi for 3.14
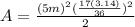
Solving the operations:
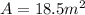
Therefore, the area is 18.5 square meters.