Question

given a line segment with endpoint a(16,8) and b(1,3) what are the coordinate of the line segment partitioned two-fifths from A to B

Answer 1

(10, 6)

Step-by-step explanation:

The x and y coordinates of a point (x, y) that partitioned a segment that goes from (x1, y1) to (x2, y2) by fraction of m/n are calculated as:

`\begin{gathered} x-\text{coordinate = }(m)/(n)(x_2-x_1)+x_1 \\ y-\text{coordinate}=(m)/(n)(y_2-y_1)+y_1 \end{gathered}`

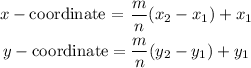
So, replacing (x1, y1) by A(16, 8), (x2, y2) by B(1, 3), and the fraction m/n by 2/5, we get

`\begin{gathered} x-\text{coordinate = }(2)/(5)(1-16)+16=(2)/(5)(-15)+16=-6+16=10 \\ y-\text{coordinate}=(2)/(5)(3-8)+8=(2)/(5)(-5)+8=6 \end{gathered}`

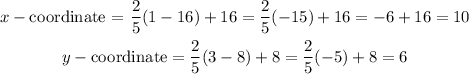
Therefore, the coordinate of the point that divided the segments into 2/5 is (10, 6).