For a normal distribution, the standard score is given by the formula:
![\begin{gathered} z=(x-\mu)/(\sigma) \\ z\colon\text{standard score} \\ x\colon\text{observed score} \\ \mu\colon\operatorname{mean}\text{ of the sample} \\ \sigma\colon\text{standard deviation of the sample} \end{gathered}]()
From the question, we are provided with the following information:
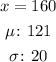
Thus, we have:
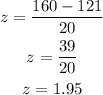
Probability of z>1.95 is 0.02558 or 2.558%
Hence, the percentage of adults in the USA that have stage 2 high blood pressure is 2.558%