Question

Compare the quantities in Column A and Column B Column A Column B The solutions of

Answer 1

Given data:

The given inequality in the column A is 4x-30≥ -3x+12.

The given inequality in the column B is 1/2 x +3 < -2x-6.

The first inequality can be written as,

`\begin{gathered} 4x-30\text{ }\ge\text{ -3x+12} \\ 7x\ge42 \\ x\ge6 \end{gathered}`

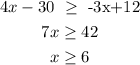
The second inequality can be written as,

`\begin{gathered} (1)/(2)x+3<-2x-6 \\ (1)/(2)x+2x<-9 \\ (5)/(2)x<-9 \\ x<-3.6 \end{gathered}`

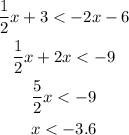
Thus, the quantity in the column A is always greater, so first option is correct.