Question

33. Suppose that the scores on a statewide standardized test are normally distributed with a mean of 70 and a standard deviation of 5. Estimate the percentage of scores that were(a) between 65 and 75. %(b) above 80. %(c) below 55. %(d) between 65 and 80. %

Answer 1

(a) 68.27%

(b) 2.28%

(c) 0.13%

(d) 81.85%

Explanation:

We have the following information:

`\begin{gathered} m=70 \\ sd=5 \end{gathered}`

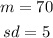
To calculate the probability we must calculate the z-value, which we do by means of the following formula:

`Z=(x-m)/(sd)`

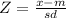
Then, with the value of Z and the help of the normal distribution table, we can calculate the probability.

The table is as follows:

Now, we calculate the probability in each case using the information above.

(a)

between 65 and 75:

`\begin{gathered} P(65\le x\le70)=(65-70)/(5)\le x\le(75-70)/(5) \\ P(65\le x\le70)=-1\le x\le1 \\ P=0.8413-0.1587=0.6827 \end{gathered}`

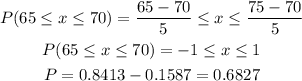
68.27% between 65 and 75.

(b)

above 80:

`\begin{gathered} P(x>80)=x>(80-70)/(5) \\ P(x>80)=x>2\rightarrow1-x<2 \\ P=1-0.9772=0.0228 \end{gathered}`

2.28% above 80.

(c)

below 55:

`\begin{gathered} P(x<55)=x<(55-70)/(5) \\ P(x<55)=x<-3 \\ P=0.0013 \end{gathered}`

0.13% below 55.

(d)

between 65 and 80:

`\begin{gathered} P(65\le x\le80)=(65-70)/(5)\le x\le(80-70)/(5) \\ P(65\le x\le80)=-1\le x\le2 \\ P=0.9772-0.1587=0.8185 \end{gathered}`

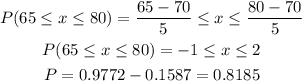
81.85% between 65 and 80.