Question

Find the perimeter of the shaded region of this composite figure.You can use 3.14 for pi.Also round your answer to the nearest hundreth.

Answer 1

In the given figure there is a rectangle, and the semi circle at one side of the rectangle so, the diameter of the circle is equal to the length of the rectangle:

SInce semi circle is inscribed in the rectangel so,

`\text{Perimeter of Shaded region=Perimeter of Rectangle without one side+Perimeter of Semicircle}`

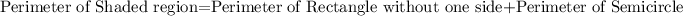
In the given figure the Length of the rectangle : 6m

Breadth of rectangle : 8m

Expression for the perimeter of rectangle is:

`\begin{gathered} \text{ Perimeter of Rectangle = 2}*(Length+breadth) \\ \text{Substitute the value of length and breadth from the given data} \\ \text{Perimeter of given rectangle = 2(6+8)} \\ \text{Perimeter of given rectangle = 28m} \end{gathered}`

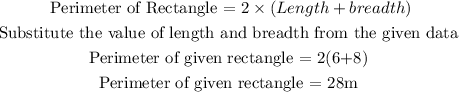
Perimeter of the circle is aslo known as the circumference of the circle So

The expression for the Circumference of the circle is :

`\begin{gathered} \text{ Circumference of Circle =2 }*\Pi*\text{ Radius} \\ \text{ Since, Semicircle is the half of the circle} \\ S\text{o, the circumference of the semicircle is the half of the circumference of the circle} \\ \text{Circumference of the semi circle=}\frac{\text{2 }*\Pi*\text{ Radius}}{2} \\ \text{Circumference of the semicircle=}\Pi*\text{ Radius} \\ \text{ From the given figure the Diameter of the semi circle is the length of the rectangle SO,} \\ \text{Diamter of semicircle=6m} \\ \text{Radius is the half of the diameter} \\ So,\text{ Radius of Semicircle =}(6)/(2)m \\ \text{Radius of Semicircle =3m} \\ \text{Substitute the value of radius in the expression of circumference} \\ \text{Circumfrence of Given semicircle is : }\Pi*3m \\ \text{ SInce }\Pi=3.14 \\ \text{Circumference of the given semicircle = 9.42m} \end{gathered}`

Now, for the perimeter of the shaded region

The perimeter of the shaded region

In the given figure of shaded region we have , 2 breadth of 8m each , one length of 6m and the circumference of the semicircle

So, the perimeter will be :

Answer :

Perimeter of the shaded region is 31.42 m