What is the correct classification for the following two linear equations?-2x + y =3y = -1/2 x-2A. Parallel Lines B. Perpendicular Lines

Question

asked Feb 23, 2023 75.5k views

1 Answer

Blair Davidson · Answer 1 · 2023-03-02T00:48:32+0000

Solution

we are given the two linear equations

First Equation

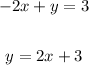
$\begin{gathered} -2x+y=3 \\ \\ y=2x+3 \end{gathered}$

Second Equation

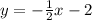
Let mA and mB denotes the gradient of the first and second equation respectively written as

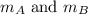
$m_A\text{ and }m_B$

Using the slope - intercepty form, one can see that

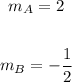
$\begin{gathered} m_A=2 \\ \\ m_B=-(1)/(2) \end{gathered}$

Now,

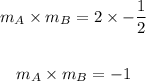
$\begin{gathered} m_A* m_B=2*-(1)/(2) \\ \\ m_A* m_B=-1 \end{gathered}$

Therefore, the lines are Perpendicular

Option B