(1) No the period of the pendulum swing depends on the mass of the bob.
(2) Yes, the period of the pendulum swing did depend on the length of the string.
(3) The data from the experiment is consistent with the pendulum equation.
Question 1:
No, the period of the pendulum swing did not depend on the mass of the bob. We can see this from the fact that the periods for the different masses at each pendulum length are approximately the same. For example, the periods for the 30 cm pendulum are 1.05 seconds for 25 grams, 1.01 seconds for 50 grams, and 1.03 seconds for 100 grams. The differences in period are small and could be due to experimental error.
Question 2:
Yes, the period of the pendulum swing did depend on the length of the string. The longer the string, the longer the period. This can be seen from the fact that the periods for the different lengths of the pendulum at each mass are all different. For example, the periods for the 25 gram bob are 1.05 seconds for a 30 cm pendulum, 1.35 seconds for a 50 cm pendulum, and 1.68 seconds for a 70 cm pendulum.
Question 3:
The pendulum equation is:

T = 2π√L/g
where T is the period, L is the length of the pendulum, and g is the acceleration due to gravity.
The data from the experiment is consistent with the pendulum equation. For example, if we calculate the period for the 30 cm pendulum using the pendulum equation, we get:
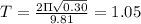 seconds
seconds
This is the same period that we measured for the 30 cm pendulum with a 25 gram bob.
We can do the same calculation for the other pendulum lengths and masses, and we get results that are consistent with the experimental data.
Therefore, the data from the experiment supports the pendulum equation.