Question

There is a raffle with 100 tickets. One ticket will win a $700 prize, one ticket will win a $510 prize, one ticket will win a $490 prize, and the remaining tickets will win nothing. If you have a ticket, what is the expected payoff?

Answer 1

`\text{\$17}`

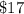
Step-by-step explanation

We want to find the expected payoff.

To do this, we have to first find the probability of winning each prize:

=> 1 ticket out of 100 will win $700 prize. The probability of winning this prize is:

`P(700)=(1)/(100)`

=> 1 ticket out of 100 will win $510 prize. The probability of winning this prize is:

`P(510)=(1)/(100)`

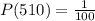
=> 1 ticket out of 100 will win $490 prize. The probability of winning this prize is:

`P(490)=(1)/(100)`

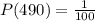
=> The remaining tickets (97) will win nothing ($0). The probability of winning $0 is:

`P(0)=(97)/(100)`

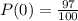
The expected value is the sum of the product of each possible outcome and its corresponding probability:

`\begin{gathered} E(X)=\Sigma\mleft\lbrace X\cdot P(X\mright)\} \\ \Rightarrow E(X)=((1)/(100)\cdot700)+((1)/(100)\cdot510)+((1)/(100)\cdot490)+((97)/(100)\cdot0) \\ E(X)=7+5.10+4.90+0 \\ E(X)=\text{ \$17} \end{gathered}`

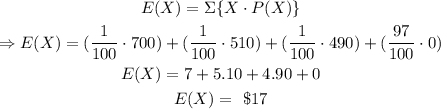
That is the expected payoff.